ETC5523: Communicating with Data

Statistical model outputs

Lecturer: Michael Lydeamore

Department of Econometrics and Business Statistics



Aim

  • Extract information from model objects
  • Understand and create functions in R

Why

  • Working with model objects is necessary for you to get the information you need for communication
  • These concepts will be helpful later when we start developing R-packages

📈 Statistical models

  • All models are approximations of the unknown data generating process
  • How good of an approximation depends on the collected data and the model choice

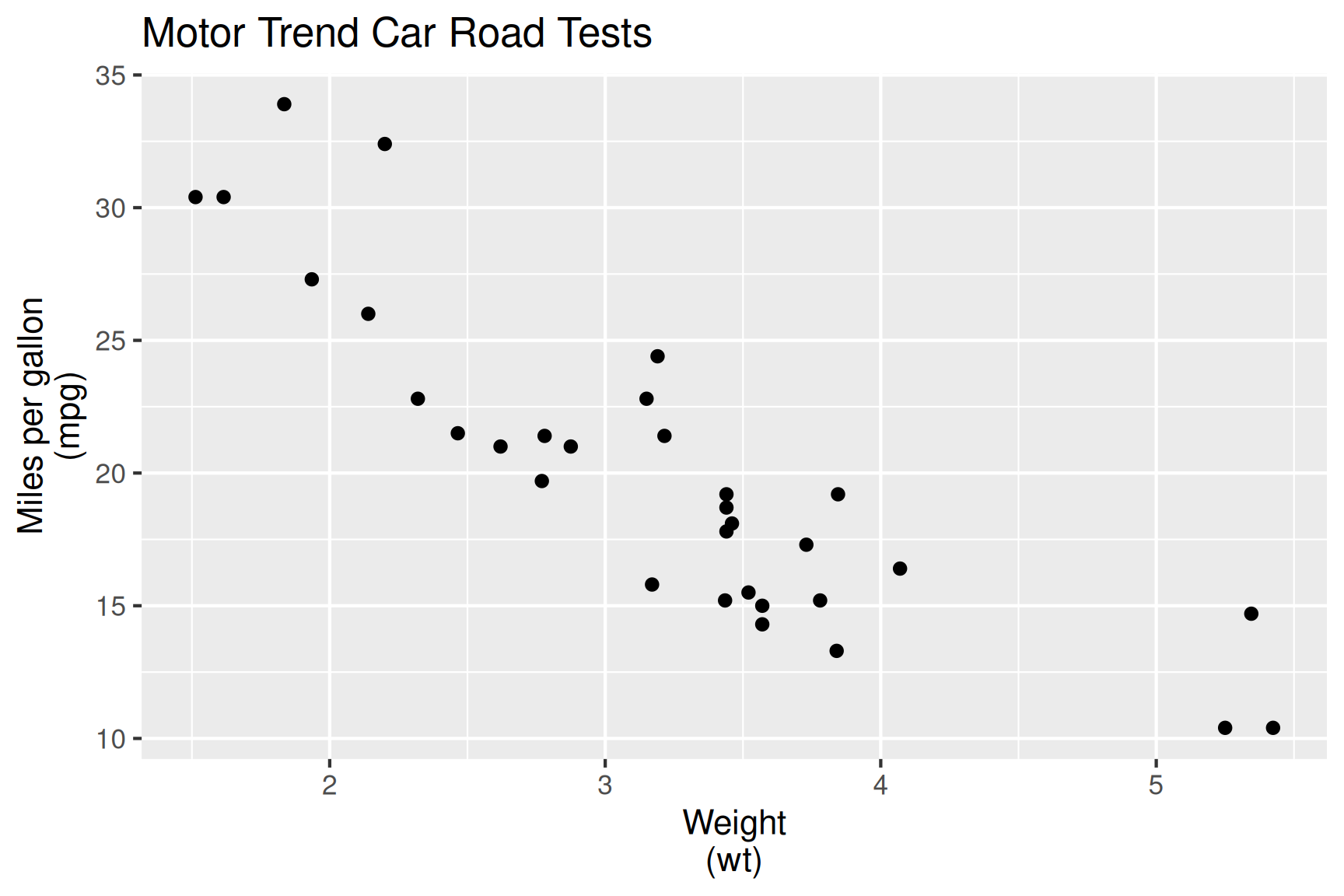
🎯 Characterise mpg in terms of wt.

Fitting linear models in R

We fit the model:

\[\texttt{mpg}_i = \beta_0 + \beta_1\texttt{wt}_i + e_i\]

In R we fit this as

fit <- lm(mpg ~ wt, data = mtcars)

\(\hat{\beta}_0 = 37.285\) and \(\hat{\beta}_1 = -5.344\)

ℹ️ Extracting information from the fitted model

  • When you fit a model, there would be a number of information you will be interested in extracting from the fit including:
    • the model parameter estimates,
    • model-related summary statistics, e.g. \(R^2\), AIC and BIC,
    • model-related values, e.g. residuals, fitted values and predictions.
  • So how do you extract these values from the fit?
  • What does fit even contain?

ℹ️ Extracting information from the fitted model

str(fit)
List of 12
 $ coefficients : Named num [1:2] 37.29 -5.34
  ..- attr(*, "names")= chr [1:2] "(Intercept)" "wt"
 $ residuals    : Named num [1:32] -2.28 -0.92 -2.09 1.3 -0.2 ...
  ..- attr(*, "names")= chr [1:32] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet 4 Drive" ...
 $ effects      : Named num [1:32] -113.65 -29.116 -1.661 1.631 0.111 ...
  ..- attr(*, "names")= chr [1:32] "(Intercept)" "wt" "" "" ...
 $ rank         : int 2
 $ fitted.values: Named num [1:32] 23.3 21.9 24.9 20.1 18.9 ...
  ..- attr(*, "names")= chr [1:32] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet 4 Drive" ...
 $ assign       : int [1:2] 0 1
 $ qr           :List of 5
  ..$ qr   : num [1:32, 1:2] -5.657 0.177 0.177 0.177 0.177 ...
  .. ..- attr(*, "dimnames")=List of 2
  .. .. ..$ : chr [1:32] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet 4 Drive" ...
  .. .. ..$ : chr [1:2] "(Intercept)" "wt"
  .. ..- attr(*, "assign")= int [1:2] 0 1
  ..$ qraux: num [1:2] 1.18 1.05
  ..$ pivot: int [1:2] 1 2
  ..$ tol  : num 1e-07
  ..$ rank : int 2
  ..- attr(*, "class")= chr "qr"
 $ df.residual  : int 30
 $ xlevels      : Named list()
 $ call         : language lm(formula = mpg ~ wt, data = mtcars)
 $ terms        :Classes 'terms', 'formula'  language mpg ~ wt
  .. ..- attr(*, "variables")= language list(mpg, wt)
  .. ..- attr(*, "factors")= int [1:2, 1] 0 1
  .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. ..$ : chr [1:2] "mpg" "wt"
  .. .. .. ..$ : chr "wt"
  .. ..- attr(*, "term.labels")= chr "wt"
  .. ..- attr(*, "order")= int 1
  .. ..- attr(*, "intercept")= int 1
  .. ..- attr(*, "response")= int 1
  .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
  .. ..- attr(*, "predvars")= language list(mpg, wt)
  .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
  .. .. ..- attr(*, "names")= chr [1:2] "mpg" "wt"
 $ model        :'data.frame':  32 obs. of  2 variables:
  ..$ mpg: num [1:32] 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
  ..$ wt : num [1:32] 2.62 2.88 2.32 3.21 3.44 ...
  ..- attr(*, "terms")=Classes 'terms', 'formula'  language mpg ~ wt
  .. .. ..- attr(*, "variables")= language list(mpg, wt)
  .. .. ..- attr(*, "factors")= int [1:2, 1] 0 1
  .. .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. .. ..$ : chr [1:2] "mpg" "wt"
  .. .. .. .. ..$ : chr "wt"
  .. .. ..- attr(*, "term.labels")= chr "wt"
  .. .. ..- attr(*, "order")= int 1
  .. .. ..- attr(*, "intercept")= int 1
  .. .. ..- attr(*, "response")= int 1
  .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
  .. .. ..- attr(*, "predvars")= language list(mpg, wt)
  .. .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
  .. .. .. ..- attr(*, "names")= chr [1:2] "mpg" "wt"
 - attr(*, "class")= chr "lm"

ℹ️ Extracting information from the fitted model

Accessing model parameter estimates:

fit$coefficients
(Intercept)          wt 
  37.285126   -5.344472 
# OR using
coef(fit)
(Intercept)          wt 
  37.285126   -5.344472

This gives us the estimates of \(\beta_0\) and \(\beta_1\).

But what about \(\sigma^2\)? Recall \(e_i \sim NID(0, \sigma^2)\).

sigma(fit)^2
[1] 9.277398

ℹ️ Extracting information from the fitted model

You can also get a summary of the model object:

summary(fit)

Call:
lm(formula = mpg ~ wt, data = mtcars)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.5432 -2.3647 -0.1252  1.4096  6.8727 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  37.2851     1.8776  19.858  < 2e-16 ***
wt           -5.3445     0.5591  -9.559 1.29e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.046 on 30 degrees of freedom
Multiple R-squared:  0.7528,    Adjusted R-squared:  0.7446 
F-statistic: 91.38 on 1 and 30 DF,  p-value: 1.294e-10

So how do I extract these summary values out?

Model objects to tidy data

broom::tidy(fit)
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    37.3      1.88      19.9  8.24e-19
2 wt             -5.34     0.559     -9.56 1.29e-10
broom::glance(fit)
# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.753         0.745  3.05      91.4 1.29e-10     1  -80.0  166.  170.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>
broom::augment(fit)
# A tibble: 32 × 9
   .rownames           mpg    wt .fitted .resid   .hat .sigma .cooksd .std.resid
   <chr>             <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>      <dbl>
 1 Mazda RX4          21    2.62    23.3 -2.28  0.0433   3.07 1.33e-2    -0.766 
 2 Mazda RX4 Wag      21    2.88    21.9 -0.920 0.0352   3.09 1.72e-3    -0.307 
 3 Datsun 710         22.8  2.32    24.9 -2.09  0.0584   3.07 1.54e-2    -0.706 
 4 Hornet 4 Drive     21.4  3.22    20.1  1.30  0.0313   3.09 3.02e-3     0.433 
 5 Hornet Sportabout  18.7  3.44    18.9 -0.200 0.0329   3.10 7.60e-5    -0.0668
 6 Valiant            18.1  3.46    18.8 -0.693 0.0332   3.10 9.21e-4    -0.231 
 7 Duster 360         14.3  3.57    18.2 -3.91  0.0354   3.01 3.13e-2    -1.31  
 8 Merc 240D          24.4  3.19    20.2  4.16  0.0313   3.00 3.11e-2     1.39  
 9 Merc 230           22.8  3.15    20.5  2.35  0.0314   3.07 9.96e-3     0.784 
10 Merc 280           19.2  3.44    18.9  0.300 0.0329   3.10 1.71e-4     0.100 
# ℹ 22 more rows

But how do these functions work?

Some common tables

Descriptive summary statistics tables

library(tidyverse)
mtcars %>% 
  select(mpg, wt, vs, cyl) %>% 
  glimpse()
Rows: 32
Columns: 4
$ mpg <dbl> 21.0, 21.0, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19.2, 17.8, …
$ wt  <dbl> 2.620, 2.875, 2.320, 3.215, 3.440, 3.460, 3.570, 3.190, 3.150, 3.4…
$ vs  <dbl> 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, …
$ cyl <dbl> 6, 6, 4, 6, 8, 6, 8, 4, 4, 6, 6, 8, 8, 8, 8, 8, 8, 4, 4, 4, 4, 8, …
4
(N=11)		 6
(N=7)		 8
(N=14)		 Overall
(N=32)
mpg
Mean (SD) 26.7 (4.51) 19.7 (1.45) 15.1 (2.56) 20.1 (6.03)
Median [Min, Max] 26.0 [21.4, 33.9] 19.7 [17.8, 21.4] 15.2 [10.4, 19.2] 19.2 [10.4, 33.9]
wt
Mean (SD) 2.29 (0.570) 3.12 (0.356) 4.00 (0.759) 3.22 (0.978)
Median [Min, Max] 2.20 [1.51, 3.19] 3.22 [2.62, 3.46] 3.76 [3.17, 5.42] 3.33 [1.51, 5.42]
vs
0 1 (9.1%) 3 (42.9%) 14 (100%) 18 (56.3%)
1 10 (90.9%) 4 (57.1%) 0 (0%) 14 (43.8%)

Regression results tables

df <- mutate(mtcars, 
             cyl = as.factor(cyl))
fit1 <- lm(mpg ~ wt + vs + cyl, data = df)
fit2 <- lm(mpg ~ wt + cyl,  data = df)

Characteristic

fit1

fit2

Beta

95% CI

1

p-value

Beta

95% CI

1

p-value
wt -3.3 -4.9, -1.7 <0.001 -3.2 -4.7, -1.7 <0.001
vs 0.86 -2.5, 4.2 0.6


cyl





    4 — —
— —
    6 -3.9 -7.1, -0.67 0.020 -4.3 -7.1, -1.4 0.005
    8 -5.1 -10, -0.10 0.046 -6.1 -9.5, -2.7 <0.001
1

CI = Confidence Interval

What statistics to present?

  • This depends on what you want to convey and your audience.

  • There are two key purposes of the table:

    1. display information; and
    2. communicate information.

  • In general, tables tend to be about display of information and graphs are preferred for communication.

  • However, if precision matters then tables can be better at communicating this than graphs.

Descriptive summary statistics

  • The main goal is to give a numerical summary to give a “feel” of what the data contains. These generally should convey:
    • variables in the data,
    • the number of observations for each variable,
    • missing values (if any),
    • the distribution, e.g. in the form of five number of summaries or counts/percentages for categorical variables.

Descriptive summary statistics

  • For numerical variables, you may have a correlation table which displays the correlation coefficients of every pair of variables. Because it is symmetrical, you can omit out the upper triangle.
Variables Mean SD 1. 2.
1. Miles per gallon 20.09 6.03
2. Weight 3.22 0.98 -0.87
3. Horsepower 146.69 68.56 -0.78 0.66

Descriptive summary statistics

  • You may have cross-tabulations (also called contingency tables)
cyl/gear 3 4 5 Total
4 3.1% (1) 25.0% (8) 6.2% (2) 34.4% (11)
6 6.2% (2) 12.5% (4) 3.1% (1) 21.9% (7)
8 37.5% (12) 0.0% (0) 6.2% (2) 43.8% (14)
Total 46.9% (15) 37.5% (12) 15.6% (5) 100.0% (32)

Regression results

  • Or more generally, the important numerical characteristics of your model. This may include:
    • parameter estimates of your model,
    • the standard error or confidence/credible interval of your estimates,
    • model fit quality, e.g. \(R^2\), AIC, BIC and so on.
  • You see often the inclusion of \(p\)-value, usually from the significance test of the corresponding variable and some indicate the significance level by the amount of *.
  • It is important to convey the uncertainty for the estimates or predictions from your model.

Regression results

  • There is also what is called the ANOVA table that shows the variation according to different sources.
glimpse(ToothGrowth)
Rows: 60
Columns: 3
$ len  <dbl> 4.2, 11.5, 7.3, 5.8, 6.4, 10.0, 11.2, 11.2, 5.2, 7.0, 16.5, 16.5,…
$ supp <fct> VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, V…
$ dose <dbl> 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0, 1.0, 1.0, …
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.350 205.35000 15.571979 0.0002312
factor(dose) 2 2426.434 1213.21717 91.999965 0.0000000
supp:factor(dose) 2 108.319 54.15950 4.106991 0.0218603
Residuals 54 712.106 13.18715

Communication considerations for tables

Numerical precision

  • Select an appropriate precision for your goal and audience:
Weight
Car brand 5 d.p. 2 d.p. 0 d.p.
Mazda RX4 2.61937 2.62 3
Mazda RX4 Wag 2.87518 2.88 3
Datsun 710 2.31916 2.32 2
Hornet 4 Drive 3.21660 3.21 3

Numerical precision

  • Display trailing zeroes to match selected precision of the column:
Trailing zeroes
Yes No
0.233 0.233
0.320 0.32
0.400 0.4
0.343 0.343

Numerical precision

  • Change and display units as appropriate:
Car brand Weight (lbs) Weight (1000 lbs) Weight (kg) Weight (g) Weight (mg)
Mazda RX4 2620 2.620 1188 1190000 1,188,000,000
Mazda RX4 Wag 2875 2.875 1304 1300000 1,304,000,000
Datsun 710 2320 2.320 1052 1050000 1,052,000,000
Hornet 4 Drive 3215 3.215 1458 1460000 1,458,000,000
  • Show comma every 3 digits (or other marks as needed).
    E.g. 1000000 is harder to read than 1,000,000.
scales::comma(c(439024, 4900343), accuracy = 1000)
[1] "439,000"   "4,900,000"

Column alignment

  • Spanner labels are usually aligned in center.
  • Right-align numbers
  • Left-align texts
Car brand
Horsepower
Left Center Right Left Center Right
Mazda RX4 Mazda RX4 Mazda RX4 110 110 110
Mazda RX4 Wag Mazda RX4 Wag Mazda RX4 Wag 110 110 110
Datsun 710 Datsun 710 Datsun 710 93 93 93
Hornet 4 Drive Hornet 4 Drive Hornet 4 Drive 110 110 110

Labels within tables

  • It is possibly obvious, but tables designed as final product (e.g. in report) should have polished labels
  • For columns, the unit may be written in the column header label
  • You shouldn’t label the unit within the table
✅
Car brand Weight<br> (1000 lbs) Displacement<br> (cubic inches)
Mazda RX4 2.620 160
Mazda RX4 Wag 2.875 160
Datsun 710 2.320 108
Hornet 4 Drive 3.215 258
Hornet Sportabout 3.440 360
Valiant 3.460 225
❌
car wt disp
Mazda RX4 2620 lbs 160 cubic inches
Mazda RX4 Wag 2875 lbs 160 cubic inches
Datsun 710 2320 lbs 108 cubic inches
Hornet 4 Drive 3215 lbs 258 cubic inches
Hornet Sportabout 3440 lbs 360 cubic inches
Valiant 3460 lbs 225 cubic inches

Texts accompanying tables

  • Besides the contents of table, a table may be accompanied with: table header, caption, footnotes and/or source notes.
  • The conventions of how and what to write will depend on your audience and medium of report
  • Generally if you are communicating information, your caption should:
    • summarise the take-away message, in other words, why should the audience care about this table?
    • give context of the table (e.g. “\(R_0 > 1\) means that the virus is more infectious”)

Making tables with R

🏗️ How to make tables in R?

  • There are many packages that make table in R, including ones that wrangle the data for you to make specialised table output. E.g. knitr::kable, kableExtra, formattable, gt, DT, pander, xtable, stargazer.

  • You can read the documentation for each packages to make the table you want (I mainly use knitr::kable, kableExtra and DT).

  • Whatever package you use, it’s important that you understand the output and how it works with the medium you are trying to display the table.

Table in Markdown

In markdown file:


First Header  | Second Header
------------- | -------------
Content Cell  | Content Cell
Content Cell  | Content Cell

Possible display:


First Header Second Header
Content Cell Content Cell
Content Cell Content Cell

Table in HTML & PDF

HTML → Web browser

<table>
<thead>
<tr>
<th>First Header</th> <th>Second Header</th>
</tr>
</thead>
<tbody>
<tr>
<td>Content Cell</td> <td>Content Cell</td>
</tr>
<tr>
<td>Content Cell</td> <td>Content Cell</td>
</tr>
</tbody>
</table>

LaTeX → PDF

\begin{tabular}{cc}
\hline
First Header & Second Header\\
\hline
Content Cell & Content Cell\\
Content Cell & Content Cell\\
\hline
\end{tabular}
  • HTML is for HTML output
  • LaTeX is for PDF output
  • Most HTML elements do not work in LaTeX and vice versa.

Case study: building static tables by components with gt

Source: https://gt.rstudio.com/

Case study: building static tables by components with gt

library(gt)
df <- select(head(mtcars), wt, disp, cyl)

Case study: building static tables by components with gt

library(gt)
df <- select(head(mtcars), wt, disp, cyl)
gt(df)
wt disp cyl
2.620 160 6
2.875 160 6
2.320 108 4
3.215 258 6
3.440 360 8
3.460 225 6

Case study: building static tables by components with gt

library(gt)
df <- select(head(mtcars), wt, disp, cyl)
gt(df) %>% 
  tab_header(title = "Motor Trend Car Road Tests", 
             subtitle = "Design and performance of 1973-74 automobile models")
Motor Trend Car Road Tests
Design and performance of 1973-74 automobile models
wt disp cyl
2.620 160 6
2.875 160 6
2.320 108 4
3.215 258 6
3.440 360 8
3.460 225 6

Case study: building static tables by components with gt

library(gt)
df <- select(head(mtcars), wt, disp, cyl)
gt(df) %>% 
  tab_header(title = "Motor Trend Car Road Tests",
             subtitle = "Design and performance of 1973-74 automobile models") %>% 
  tab_source_note(md("Source: 1974 *Motor Trend* US magazine"))
Motor Trend Car Road Tests
Design and performance of 1973-74 automobile models
wt disp cyl
2.620 160 6
2.875 160 6
2.320 108 4
3.215 258 6
3.440 360 8
3.460 225 6

Source: 1974 Motor Trend US magazine

Case study: building static tables by components with gt

library(gt)
df <- select(head(mtcars), wt, disp, cyl)
gt(df) %>% 
  tab_header(title = "Motor Trend Car Road Tests",
             subtitle = "Design and performance of 1973-74 automobile models") %>% 
  tab_source_note(md("Source: 1974 *Motor Trend* US magazine")) %>% 
  cols_label( 
    wt = html("Weight<br>(1000lbs)"), 
    disp = html("Displacement<br> (inch<sup>3</sup>)"), 
    cyl = html("Number of<br>cylinders") 
  )
Motor Trend Car Road Tests
Design and performance of 1973-74 automobile models
Weight
(1000lbs)		 Displacement
(inch3)		 Number of
cylinders
2.620 160 6
2.875 160 6
2.320 108 4
3.215 258 6
3.440 360 8
3.460 225 6

Source: 1974 Motor Trend US magazine

Case study: interactive tables with DT

DT::datatable(mtcars, options = list(pageLength = 4))
  • DT::datatable works best for HTML documents.
  • For PDF documents, it takes a webshot of the HTML table and inserts it as an image.
  • It’s useful for data exploration where the main goal of the table is display of information rather than communication.

When do you make tables over plots?

  • When you want to show exact values or the accuracy of the values are important to convey.
  • You can combine plots with tables!

Case study heatmap table with formattable

library(formattable)
mtcars %>% 
  select(mpg, disp, wt, hp) %>% 
  cor() %>% 
  as.data.frame() %>% 
  rownames_to_column("Variables") %>% 
  formattable(list(area(col = 2:5) ~ color_tile("#F5B7B1", "#7DCEA0")))
Variables mpg disp wt hp
mpg 1.0000000 -0.8475514 -0.8676594 -0.7761684
disp -0.8475514 1.0000000 0.8879799 0.7909486
wt -0.8676594 0.8879799 1.0000000 0.6587479
hp -0.7761684 0.7909486 0.6587479 1.0000000

Case study: inline plots with sparkline

  • Sparkline refers to a small chart drawn without axes or coordinates.
  • This will be out of scope for this unit.

Week 5 Lesson

Summary

  • You saw various common tables that present information and the motivation behind it
  • We went through some guidelines for best way to communicate with tables

Resources

ETC5523 Week 5A