ETC5523: Communicating with Data

Tutorial 5

Author

Michael Lydeamore

Published

1 May 2001

๐ŸŽฏ Objectives

  • create new functions and generic methods
  • understand and follow guidelines for best way to communicate with tables
  • construct regression, descriptive, and interactive tables with R Markdown
  • deconstruct and manipulate โ€œnovelโ€ model objects
  • modify the look of HTML tables produced by R Markdown or Quarto

Install the R-packages

install.packages(c("broom", "DT", "kableExtra", "palmerpenguins", "modelsummary", "gtsummary"))

๐Ÿ‘ฅ Exercise 5A

Reporting regression tables

Create regression tables, respecting the standard guidelines of presentation for tables, with models lm1 and rlm1 below using modelsummary, gtsummary or otherwise.

๐Ÿ› ๏ธ Exercise 5B

Interactive data tables

Produce the same table that you find below using DT using the penguins data in the palmerpenguins package.

๐Ÿ‘ฅ Exercise 5C - Challenge

Working with robust linear models

Consider the artificial data in the object df. There are two obvious outliers. Which observations are the outliers?

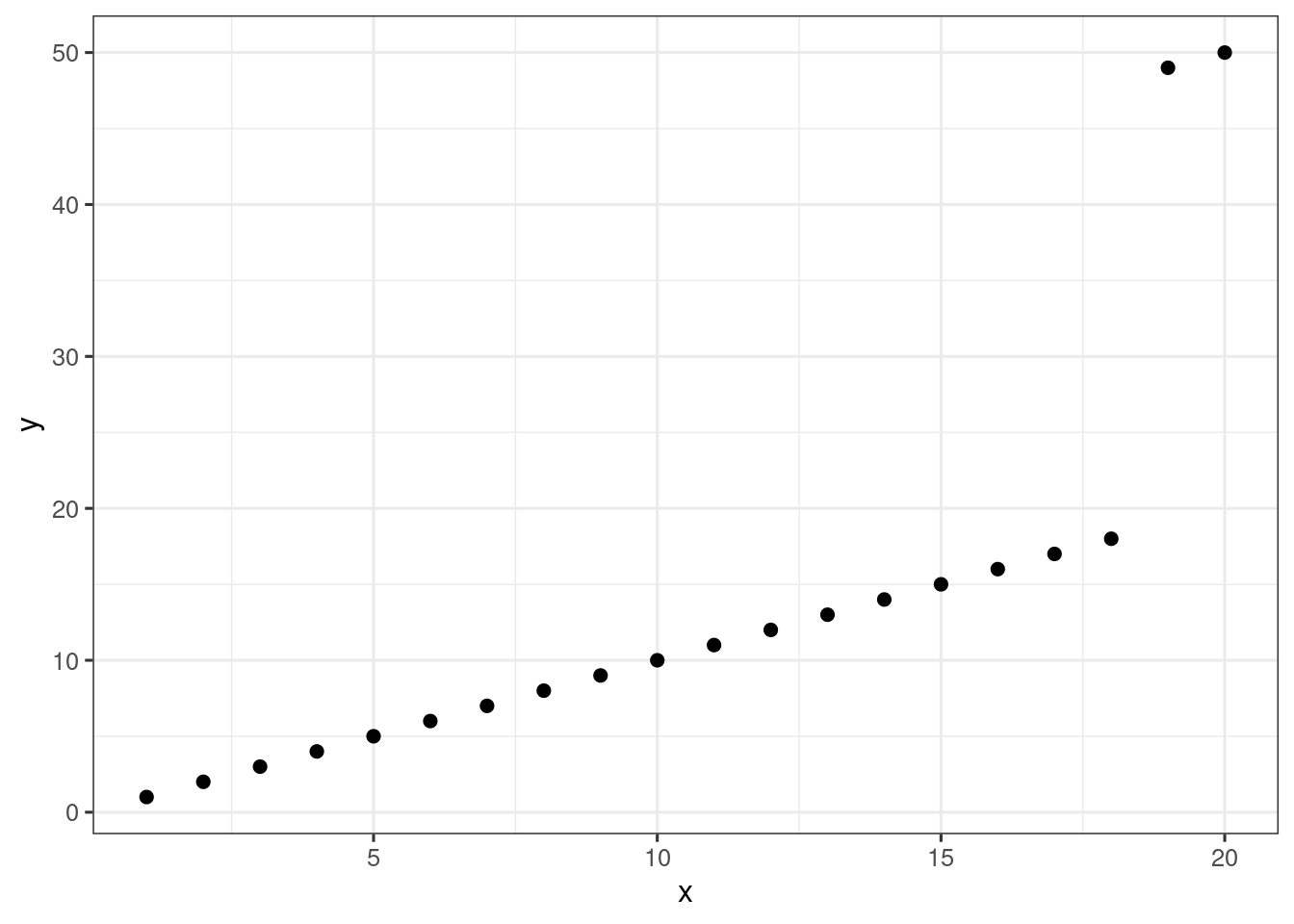
A simple linear model where parameters are estimated using least squares estimate are not robust to outliers. Below we fit two models:

  1. a linear model with least square estimates contained in fit_lm and
  2. a robust linear model contained in fit_rlm.

To explain briefly, a robust linear model down-weights the contribution of the observations that are outlying observations to estimate parameters.

fit_lm <- lm(y ~ x, data = df) 
fit_rlm <- rlm(y ~ x, data = df)

Below is a modification to the augment method from the broom package to extract some model-related values and the weights from the iterated re-weighted least squares.

augment.rlm <- function(fit, ...) {
   broom:::augment.rlm(fit) %>% 
    mutate(w = fit$w)
}

augment(fit_rlm)
# A tibble: 20 ร— 9
       y     x .fitted     .resid      .hat .sigma .cooksd .std.resid         w
   <int> <int>   <dbl>      <dbl>     <dbl>  <dbl>   <dbl>      <dbl>     <dbl>
 1     1     1   0.999  0.000546  0.206      10.3       NA         NA 1        
 2     2     2   2.00   0.000452  0.172      10.3       NA         NA 1        
 3     3     3   3.00   0.000358  0.143      10.3       NA         NA 1        
 4     4     4   4.00   0.000263  0.118      10.3       NA         NA 1        
 5     5     5   5.00   0.000169  0.0974     10.3       NA         NA 1        
 6     6     6   6.00   0.0000749 0.0808     10.3       NA         NA 1        
 7     7     7   7.00  -0.0000193 0.0685     10.3       NA         NA 1        
 8     8     8   8.00  -0.000114  0.0603     10.3       NA         NA 1        
 9     9     9   9.00  -0.000208  0.0564     10.3       NA         NA 1        
10    10    10  10.0   -0.000302  0.0566     10.3       NA         NA 1        
11    11    11  11.0   -0.000396  0.0611     10.3       NA         NA 1        
12    12    12  12.0   -0.000490  0.0698     10.3       NA         NA 1        
13    13    13  13.0   -0.000585  0.0827     10.3       NA         NA 1        
14    14    14  14.0   -0.000679  0.0998     10.3       NA         NA 1        
15    15    15  15.0   -0.000773  0.121      10.3       NA         NA 1        
16    16    16  16.0   -0.000867  0.147      10.3       NA         NA 1        
17    17    17  17.0   -0.000961  0.172      10.3       NA         NA 0.977    
18    18    18  18.0   -0.00106   0.187      10.3       NA         NA 0.890    
19    49    19  19.0   30.0       0.0000184   7.28      NA         NA 0.0000742
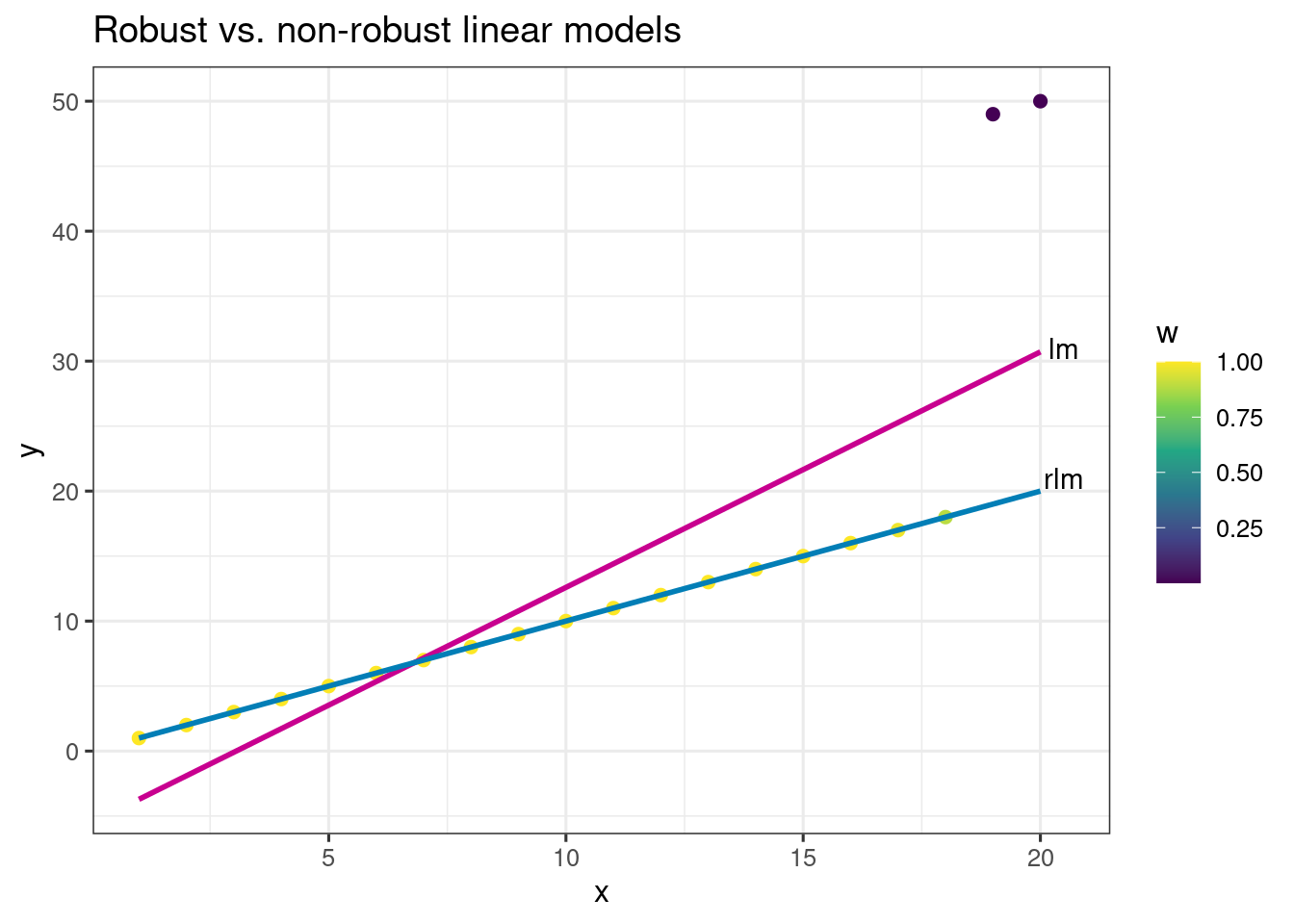
20    50    20  20.0   30.0       0.0000216   7.28      NA         NA 0.0000742

Here is a plot to compare the two model fits, and to give some understanding of these weights. What do you notice about the weights?

Can you

  1. recreate this plot using the functions in this question and
  2. improve the plot to better undertstand the differences in the model and the weights?